背景
人逢喜事精神爽,总算熬到下班撩~~
正准备和同事打个招呼回家,被同事拖住问了.
🙋♂️: 你们组做的那块代码,把double类型数据成float有问题啊💨.
💁♀️: 嗯?不对是正常啊,float精度是没有double高,但float能保存到小数点后好多位,对我们来说完全够用了!
🙋♂️: 不是啊,这不是小数点多少位的问题,而是现在整型数据,转出来也有问题啊,你看.
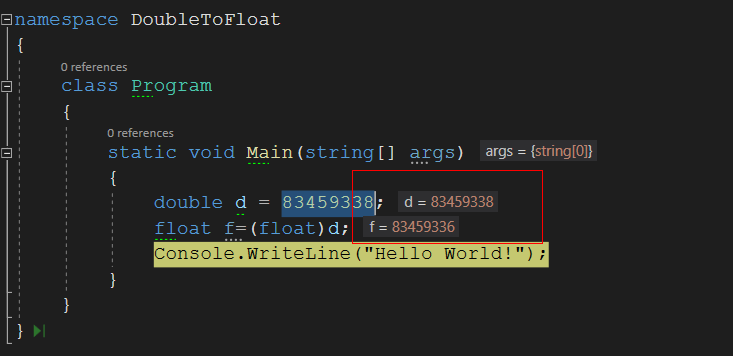
💁♀️: XX00😱… 这什么鬼?
看到这个结果,差点闪到我的老腰🤦,咋不按套路出牌呢?
然后,下班路上,感觉我好像被我挚爱的.Net欺骗了💔,double强转float用了这么多年,咋说不对就不对了?.Net不靠谱啊!
浮点类型数据的存储
当然,我内心还是相信.Net是清白的,所以刨根究底,网上找的资料大多是说这种强转会照成小数点后的精度的问题,可是造成整数位的问题精度问题却少有人提及.
为了理解这个问题,我们要从一些大学计算机基础的相关知识讲起😂.
float和double有什么不同?
- float四个字节,double八个字节.
- float范围从10-38到1038 和 -1038到-10-38, double的范围从10-308到10308 和 -10-308到-10-308
当然了,这都是废话🤷, 重点是下面这条.
- float是
单精度浮点数,double是双精度浮点数.
单精度与双精度什么区别
根据国际标准IEEE 754,任意一个二进制浮点数V可以表示成下面的形式:
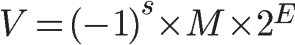
-
(-1)^s表示符号位,当s=0,V为正数;当s=1,V为负数。
-
M表示有效数字,大于等于1,小于2。
-
2^E表示指数位。
举例来说,十进制的5.0,写成二进制是101.0,相当于1.01×2^2。那么,按照上面V的格式,可以得出s=0,M=1.01,E=2。
十进制的-5.0,写成二进制是-101.0,相当于-1.01×2^2。那么,s=1,M=1.01,E=2。
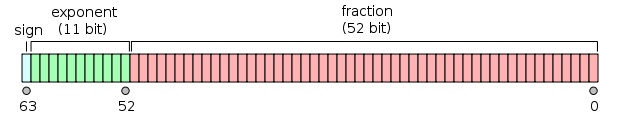
对于32位的单精度浮点数,最高的1位是符号位s,接着的8位是指数E,剩下的23位为有效数字M。

对于64位的双精度浮点数,最高的1位是符号位S,接着的11位是指数E,剩下的52位为有效数字M。
经过上面关于浮点数的介绍,相信你可能还是一头雾水,就像下面这幅漫画展示的那样🐎.
浮点数转成内存存储
为了避免产生上面那种画马的跳跃,我们一小步一小步,看看浮点数据具体怎么在内存中存储的.双精度与单精度类似,这里我以单精度为例.
- 先将这个实数的绝对值化为二进制格式。
- 将这个二进制格式实数的小数点左移或右移n位,直到小数点移动到第一个有效数字的右边。
- 从小数点右边第一位开始数出二十三位数字放入第22到第0位。
- 如果实数是正的,则在第31位放入“0”,否则放入“1”。
- ⭐如果n 是左移得到的,说明指数是正的,第30位放入“1”。如果n是右移得到的或n=0,则第30位放入“0”。
- 如果n是左移得到的,则将n减去1后化为二进制,并在左边加“0”补足七位,放入第29到第23位。如果n是右移得到的或n=0,则将n化为二进制后在左边加“0”补足七位,再各位求反,再放入第29到第23位。
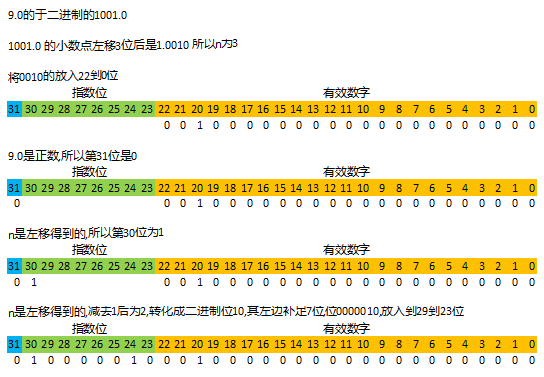
我们先用上述步骤尝试把9.0转化成二进制存储形式.
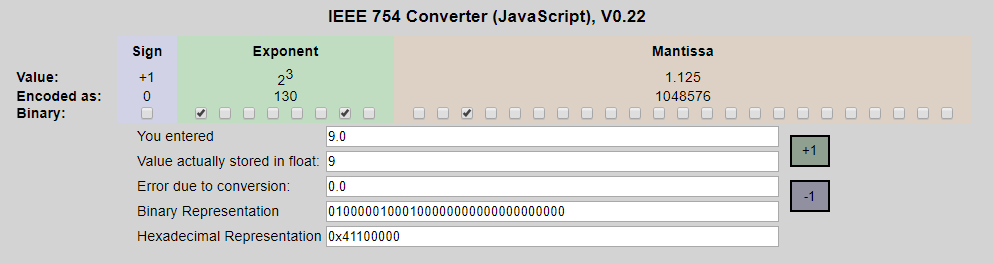
我们可以通过这个地址校验计算结果的正确性. https://www.h-schmidt.net/FloatConverter/IEEE754.html
可以看到,与我们的计算结果完全一致.
翻车分析
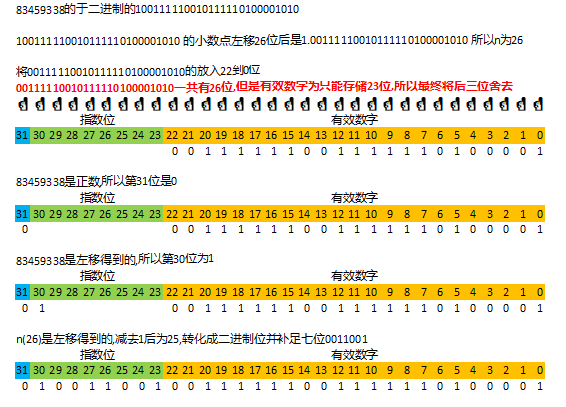
现在我们用上面的步骤,把照成翻车的83459338转成内存存储形式看看.
通过在线工具转换后证实我们的转换完全正确.
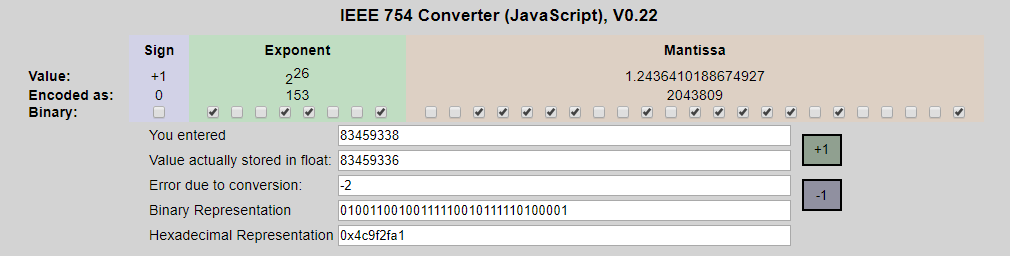
然后我们再把数据转回来.
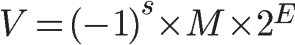
S是第31位,为0, E =0011001(25)+1=26, 重点在M,它是1.(有效数字位)即 1.00111110010111110100001
1.00111110010111110100001乘上2的26次方,为100111110010111110100001000,将其转换为十进制,为 83459336
没错,就是83459336,而不是83459338🌋
83459338=> 100111110010111110100001010
83459336=> 100111110010111110100001000
可以看到,两个数字转成成二进制后,倒数第二位产生了差异,而产生这种的差异的原因就是单精度浮点数小数位23位不足以存储所有二进制数(26位).
🚑这场事故告诉我们,强转虽好,容易翻车.




评论区